Tiệm cận đứng của đồ thị hàm số là gì? Bài viết dưới đây hướng dẫn các em học sinh cách tìm đường tιệm cận đứng của đồ thị một hàm số. Chúng ta cùng theo dõi nhé!
Đường tiệm cận đứng của đồ thị hàm số
Cho hàm số y=f(x) xác định trên K\{α}. Nếu giới hạn của hàm số f(x) khi x tiến đến “bên trái” hoặc x tiến đến “bên phải” điểm α bằng vô cực (âm vô cực hoặc dương vô cực). Thì đồ thị hàm số y=f(x) có đường tιệm cận đứng là x=α.
Theo cách hiểu như vậy các em cần lưu ý để x có thể tiến đến α thì f(x) phải xác định trên lân cận trái (hoặc phải) của điểm α.
Chẳng hạn như f(x) có tập xác định là (1;3) và không xác định tại x=5 thì x không thể tiến tới giá trị 5 được. Vì vậy cũng không thể có tιệm cận đứng x=5.

Tìm tiệm cận đứng của đồ thị hàm số
Tìm tiệm đứng bao gồm các bước sau:
- Bước 1. Tìm tập xác định của hàm số.
- Bước 2. Tìm những điểm mà hàm số không xác định nhưng có lân cận trái hoặc lân cận phải của điểm đó nằm trong tập xác định.
- Bước 3. Tính các giới hạn một bên của hàm số tại các điểm ở bước 2 và kết luận theo định nghĩa nêu trên.
Ví dụ:
Tìm tiệm cận đứng của hàm số sau:
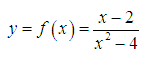
Lời giải:

Công thức tiệm cận đứng của hàm số phân tuyến tính
Cách tìm tιệm cận đứng của hàm phân tuyến tính y=(ax+b)/(cx+d) (ad−bc≠0, c≠0) có thể được tính nhanh thông qua công thức. Cụ thể hàm số phân tuyến tính có một đường tιệm cận đứng duy nhất là x=−d/c.

Ví dụ:
Hàm số y=(x−2)/(x+3) có duy nhất một đường tιệm cận đứng là x=−3.