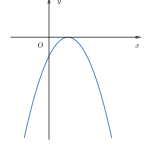
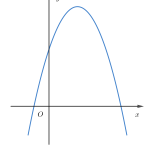
Cách vẽ đồ thị hàm số bậc 2 ở lớp 10 như thế nào? Bài viết dưới đây sẽ hướng dẫn các em vẽ đồ thị hàm số bậc hai theo cách ở lớp 10.
Hhảo sát và vẽ đồ thị hàm số bậc 2
Hàm số bậc 2 là hàm số có dạng y=ax²+bx+c (a≠0). Khảo sát hàm số bậc 2.
- Tập xác định: R.
- Sự biến thiên
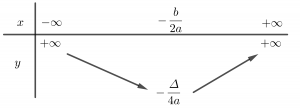
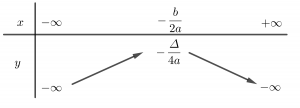
Bảng biến thiên của hàm số y=ax²+bx+c chia làm 2 trường hợp:
Trường hợp a>0, hàm số nghịch biến trên khoảng (−∞; −b/2a) và đồng biến trên khoảng (−b/2a;+∞).
Trong trường hợp a<0, hàm số đồng biến trên khoảng (−∞; −b/2a) và nghịch biến trên khoảng (−b/2a;+∞).
- Đồ thị hàm bậc 2
Đồ thị hàm bậc 2 là một Parabol.
Cách vẽ đồ thị hàm số bậc 2
Cách vẽ Parabol gồm các bước sau:
- Bước 1: Vẽ trục đối xứng: x=−b/2a. Đây là đường thẳng đi qua điểm (-b/2a;0) và song song với trục Oy.
- Bước 2: Xác định tọa độ đỉnh : (−b/2a;−delta/4a). Đây là điểm nằm trên trục đối xứng. Mẹo tính nhanh tung độ đỉnh là lấy máy tính nhập biểu thức ax²+bx+c sau đó bấm CALC −b/2a :)).
- Bước 3: Xác định thêm 1 số điểm như giao điểm với trục tung, trục hoành… Sau đó nhớ đối xứng các điểm lấy thêm qua trục nhé!
- Bước 4: Tất nhiên là vẽ đồ thị rồi. Luyện nhiều vẽ sẽ đẹp thôi. Học sinh ở quê tôi hay lấy cái lạt tre mỏng uốn cong rồi vẽ :)). Đẹp lắm nha!.
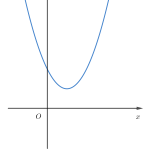
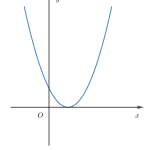
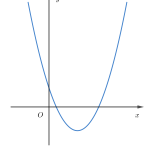
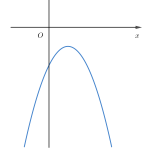
Để tránh sai sót (nhiều bạn hay gặp đó nha) là ta nhớ dáng điệu của Parabol trong các trường hợp cụ thể được minh họa ở hình dưới đây.
Các dạng đồ thị hàm số bậc hai
Đồ thị hàm số bậc hai và dấu tam thức bậc hai
Lưu ý: Số giao điểm của đồ thị hàm số bậc hai chính là số nghiệm của phương trình ax²+bx+c=0. Từ các trường hợp trên của đồ thị hàm số bậc hai ta có thể suy ra được dấu của tam thức bậc hai. Cụ thể trong 2 trường hợp delta<0 thì tam thức có dấu không đổi phụ thuộc vào hệ số a. Trong 2 trường hợp delta=0 thì tam thức có dấu không đổi phụ thuộc vào hệ số a và chỉ bằng 0 tại các nghiệm. Trường hợp delta>0 thì tam thức bậc 2 đổi dấu khi qua các nghiệm. Chúng ta vẫn thường nhớ dấu tam thức bậc 2 qua câu “Trong trái ngoài cùng bằng 0 tại nghiệm”. Nghĩa là trong khoảng 2 nghiệm thì trái dấu với hệ số a. Ngoài khoảng hai nghiệm thì cùng dấu với hệ số a. Tại hai nghiệm thì bằng 0. Khi hai nghiệm trùng nhau (nghiệm kép) hoặc vô nghiệm thì phần “trong trái” không còn nữa.